Ebene kristallographische Gruppe

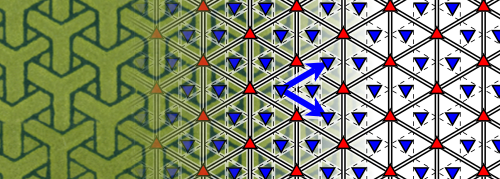
Die ebenen kristallographischen Gruppen, auch Tapetenmustergruppe, Wandmustergruppen oder Ornamentgruppen genannt, sind die Symmetriegruppen von periodischen Mustern oder Parkettierungen der euklidischen Ebene. Es gibt, bis auf affine Äquivalenz, genau 17 solche Gruppen. Ihnen entsprechen im dreidimensionalen Raum die 230 kristallographischen Raumgruppen.

Im Sinne der Gruppentheorie bestehen die Gruppen aus der Menge aller Kongruenzabbildungen, die das Muster auf sich selbst abbilden, zusammen mit der Komposition von Abbildungen als Gruppenoperation.

Symmetrieelemente

Ein periodisches Muster kann Kombinationen der folgenden elementaren Symmetrieelemente aufweisen:

1. Translation (Verschiebung)
2. Achsenspiegelung
3. Gleitspiegelung, also eine Kombination aus Translation und Achsenspiegelung
4. Rotation
   • 2-zählig, also eine Drehung um 180° bzw. eine Punktspiegelung
   • 3-zählig, also eine Drehung um 120°
   • 4-zählig, also eine Drehung um 90°
   • 6-zählig, also eine Drehung um 60°

Andere Drehungen als die aufgezählten sind unmöglich. Das liegt daran, dass (abgesehen von der zweizähligen Drehung) zu jeder Symmetriegruppe eine periodische Parkettierung der Ebene mit regelmäßigen Vielecken entsprechender Zähligkeiten gehört. Und eine Parkettierung mit beispielsweise Fünfecken ist unmöglich, weil sich aufgrund der Innenwinkelsumme ein Innenwinkel von 108° ergibt, sodass eine derartige Parkettierung an den Ecken nicht aufgehen würde (108 ist kein Teiler von 360). In nichteuklidischen Geometrien hingegen sind auch Symmetriegruppen mit anderen Zähligkeiten möglich.

Eine 4-zählige Rotationssymmetrie impliziert natürlich eine 2-zählige, genauso wie eine 6-zählige sowohl eine 3-zählige als auch eine 2-zählige impliziert. Es wird normalerweise für jedes Rotationszentrum jeweils nur der höchste Wert angegeben.

Jedes periodische Muster kann erzeugt werden, indem diese Operationen auf eine beschränkte Elementarzelle immer wieder angewandt werden, bis die gesamte Ebene parkettiert ist. Per Definition enthält die Symmetriegruppe eines periodischen Musters immer zwei linear unabhängige Translationen. Dadurch ist es auch möglich, allein durch wiederholte Verschiebung einer translativen Zelle das gesamte Muster zu erzeugen. Die translative Zelle enthält dabei eine oder mehrere Kopien der elementaren Zelle.

Notation

Orbifold-Notation

Die Eigenschaften einer Symmetriegruppe können auch durch die sogenannte Orbifold-Notation beschrieben werden.

• Ziffern n (2, 3, 4, 6) bezeichnen ein n-zähliges Rotationszentrum.
• Ein ∗ steht für eine Spiegelachse.
  • Ziffern, die vor einem ∗ stehen, liegen abseits der Spiegelachsen
  • Ziffern, die nach einem ∗ stehen, liegen auf den Spiegelachsen
• Ein × steht für eine Gleitspiegelung.
• Ein ∘ steht für keine Symmetrien, abgesehen von den Translationen.
• Die in jeder Gruppe vorkommenden Translationen werden nicht explizit notiert.

Kurzübersicht

Gruppe	Orbifold-Notation	Translationszelle (z. B.)	Elementarzellen in minimaler Translationszelle
p1	∘1	Parallelogramm	1
p2	2222	Parallelogramm	2
pm	**	Rechteck	2
pg	××	Rechteck	2
cm	∗×	Raute	2
pmm	∗2222	Rechteck	4 Rechtecke
pmg	22∗	Rechteck	4
pgg	22×	Rechteck	4
cmm	2∗22	Raute	4
p4	442	Quadrat	4
p4m	∗442	Quadrat	8 rechtwinklig gleichschenklige Dreiecke
p4g	4∗2	Quadrat	8
p3	333	Raute aus zwei gleichseitigen Dreiecken	3
p3m1	∗333	Raute aus zwei gleichseitigen Dreiecken	6 gleichseitige Dreiecke
p31m	3∗3	Raute aus zwei gleichseitigen Dreiecken	6
p6	632	Raute aus zwei gleichseitigen Dreiecken	6
p6m	∗632	Raute aus zwei gleichseitigen Dreiecken	12 rechtwinklige Dreiecke mit einem Kathetenverhältnis von 2:1

Liste

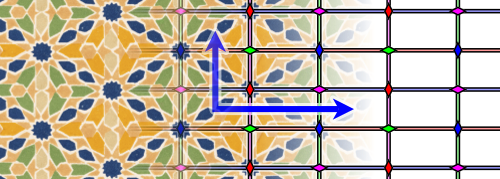
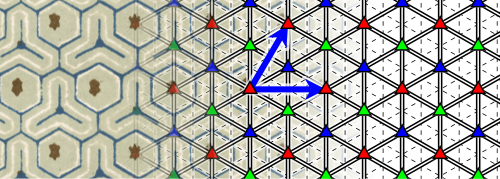
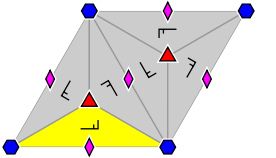
Die in den Strukturdiagrammen angegebenen Elemente sind wie folgt gekennzeichnet:

	Zentrum einer zweizähligen Rotation (180°).
	Zentrum einer dreizähligen Rotation (120°).
	Zentrum einer vierzähligen Rotation (90°).
	Zentrum einer sechszähligen Rotation (60°).
	Spiegelachse.
	Gleitspiegelachse.

Dabei sind unterschiedliche Äquivalenzklassen der Elemente durch unterschiedliche Farben und Drehungen gekennzeichnet.

Die gelb markierten Fläche kennzeichnet eine Elementarzelle, der gesamte abgebildete Bereich eine translative Zelle.

Gruppe p1

Klassen von Symmetrieelementen in p1

Rotationen				Achsen
2	3	4	6	Spiegel-	Gleitspiegel-
–	–	–	–	–	–

• Orbifold-Notation: ∘1.
• Diese Gruppe besitzt nur Verschiebung als einzige Form der Symmetrie.

Gruppe p2

Klassen von Symmetrieelementen in p2

Rotationen				Achsen
2	3	4	6	Spiegel-	Gleitspiegel-
4	–	–	–	–	–

• Orbifold-Notation: 2222.
• Diese Gruppe hat vier Klassen von Punktspiegelzentren. Diese zweizählige Drehung ist neben der Translation die einzige Symmetrieform.

Gruppe pm

Klassen von Symmetrieelementen in pm

Rotationen				Achsen
2	3	4	6	Spiegel-	Gleitspiegel-
–	–	–	–	2	–

• Orbifold-Notation: ∗∗.
• Diese Gruppe hat zwei zueinander parallele Spiegelachsen. Es existiert keine Rotationssymmetrie.

Gruppe pg

Klassen von Symmetrieelementen in pg

Rotationen				Achsen
2	3	4	6	Spiegel-	Gleitspiegel-
–	–	–	–	–	2

• Orbifold-Notation: ××.
• Diese Gruppe besitzt zwei zueinander parallele Gleitspiegelachsen. Es existiert keine Rotationssymmetrie.

Gruppe cm

Klassen von Symmetrieelementen in cm

Rotationen				Achsen
2	3	4	6	Spiegel-	Gleitspiegel-
–	–	–	–	1	1

• Orbifold-Notation: ∗×.
• Diese Gruppe hat parallel zueinander abwechselnd Spiegelachsen und Gleitspiegelachsen.

Gruppe pmm

Klassen von Symmetrieelementen in pmm

Rotationen				Achsen
2	3	4	6	Spiegel-	Gleitspiegel-
4	–	–	–	4	–

• Orbifold-Notation: ∗2222.
• Diese Gruppe zeichnet sich durch aufeinander senkrecht stehende Spiegelachsen aus. An dem Schnittpunkt zweier Spiegelachsen ergeben sich zweizählige Drehzentren. Es gibt insgesamt vier Klassen von Drehzentren und vier Klassen von Spiegelachsen.

Gruppe pmg

Klassen von Symmetrieelementen in pmg

Rotationen				Achsen
2	3	4	6	Spiegel-	Gleitspiegel-
2	–	–	–	1	2

• Orbifold-Notation: 22∗.
• Hier gibt es eine einzelne Klasse von Spiegelachsen sowie senkrecht dazu zwei verschiedene Klassen von Gleitspiegelachsen, auf denen sich zweizählige Drehzentren ergeben.

Gruppe pgg

Klassen von Symmetrieelementen in pgg

Rotationen				Achsen
2	3	4	6	Spiegel-	Gleitspiegel-
2	–	–	–	–	2

• Orbifold-Notation: 22×.
• Diese Gruppe hat keine einfache Achsensymmetrie, jedoch zwei zueinander senkrechte Gleitspiegelachsen, sowie zwei Klassen von Punktspiegelzentren.

Gruppe cmm

Klassen von Symmetrieelementen in cmm

Rotationen				Achsen
2	3	4	6	Spiegel-	Gleitspiegel-
3	–	–	–	2	2

• Orbifold-Notation: 2∗22.
• Diese Gruppe enthält zwei Klassen von Spiegelachsen, die aufeinander senkrecht stehen, mit zweizähligen Drehzentren an den Schnittpunkten. Eine zusätzliche Klasse von zweizähligen Drehzentren liegt abseits der Spiegelachsen. Dies führt auch zu zwei Klassen von Gleitspiegelachsen.

Gruppe p4

Klassen von Symmetrieelementen in p4

Rotationen				Achsen
2	3	4	6	Spiegel-	Gleitspiegel-
1	–	2	–	–	–

• Orbifold-Notation: 442.
• Diese Gruppe weist keine Form von Achsensymmetrie auf. Erkennungsmerkmal sind vierzählige Rotationen, zu denen es zwei Klassen von Zentren gibt. Dazwischen ergeben sich zweizählige Drehzentren.

Gruppe p4m

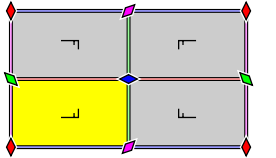
Klassen von Symmetrieelementen in p4m

Rotationen				Achsen
2	3	4	6	Spiegel-	Gleitspiegel-
1	–	2	–	3	1

• Orbifold-Notation: ∗442.
• Diese Gruppe wird auch als p4mm bezeichnet.

Gruppe p4g

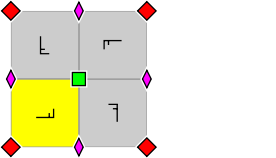
Klassen von Symmetrieelementen in p4g

Rotationen				Achsen
2	3	4	6	Spiegel-	Gleitspiegel-
1	–	1	–	1	2

• Orbifold-Notation: 4∗2.
• Diese Gruppe wird auch als p4gm bezeichnet.

Gruppe p3

Klassen von Symmetrieelementen in p3

Rotationen				Achsen
2	3	4	6	Spiegel-	Gleitspiegel-
–	3	–	–	–	–

• Orbifold-Notation: 333.

Gruppe p3m1

Klassen von Symmetrieelementen in p3m1

Rotationen				Achsen
2	3	4	6	Spiegel-	Gleitspiegel-
–	3	–	–	1	1

• Orbifold-Notation: ∗333.

Gruppe p31m

Klassen von Symmetrieelementen in p31m

Rotationen				Achsen
2	3	4	6	Spiegel-	Gleitspiegel-
–	2	–	–	1	1

• Orbifold-Notation: 3∗3.

Gruppe p6

Klassen von Symmetrieelementen in p6

Rotationen				Achsen
2	3	4	6	Spiegel-	Gleitspiegel-
1	1	–	1	–	–

• Orbifold-Notation: 632.

Gruppe p6m

Klassen von Symmetrieelementen in p6m

Rotationen				Achsen
2	3	4	6	Spiegel-	Gleitspiegel-
1	1	–	1	2	2

• Orbifold-Notation: ∗632.
• Diese Gruppe wird auch als p6mm bezeichnet.

Ornamentgruppen in der Kunst

Bei zweifach periodischen Mustern aus dem Alten Ägypten wurden 12 der 17 Ornamentgruppen nachgewiesen; es fehlen die 5 Gruppen mit 3- bzw. 6-facher Rotationssymmetrie. Die Arabesken in der Alhambra gelten als hervorragendes Beispiel der Verwendung von zweifach periodischen Mustern in der islamischen Kunst. Ob alle 17 Ornamentgruppen in der Alhambra vorkommen oder nicht, ist umstritten: Edith Müller und Branko Grünbaum sagen nein, José María Montesinos und Marcus du Sautoy sagen ja. Bis auf möglicherweise pm, p3 und pg wurden alle Ornamentgruppen in China verwendet.

Siehe auch

• Symmetrie (Geometrie)
• Punktgruppe

Literatur

• Branko Grünbaum, Geoffrey C. Shephard: Tilings and Patterns. Freeman, New York NY 1987, ISBN 0-7167-1193-1.
• Michael Klemm: Symmetrien von Ornamenten und Kristallen. Springer, Berlin u. a. 1982, ISBN 3-540-11644-3.
• Klaus Lamotke: Die Symmetriegruppen der ebenen Ornamente. In: Mathematische Semesterberichte. Band 52, Nr. 2, August 2005, S. 153–174, doi:10.1007/s00591-005-0092-y. 

Einzelnachweise

1. ↑ Branko Grünbaum: The Emperor's New Clothes: Full Regalia, G string, or Nothing? In: The Mathematical Intelligencer. Band 6, Nr. 4, 1984, S. 47–53, doi:10.1007/BF03026738.
2. ↑ Edith Müller: Gruppentheoretische und strukturanalytische Untersuchungen der maurischen Ornamente aus der Alhambra in Granada. Baublatt, Rüschlikon 1944 (Zugleich: Zürich, Universität, Dissertation, 1944).
3. ↑ Branko Grünbaum: What Symmetry Groups Are Present in the Alhambra? In: Notices of the American Mathematical Society. Band 53, Nr. 6, 2006, ISSN 0002-9920, S. 670–673, Digitalisat (PDF; 1,97 MB).
4. ↑ José M. Montesinos: Classical Tesselations and Three-Manifolds. Springer, Berlin u. a. 1987, ISBN 3-540-15291-1.
5. ↑ Marcus du Sautoy: Finding Moonshine. A Mathematician's Journey through Symmetry. Fourth Estate, London 2008, ISBN 978-0-00-721461-7, Kapitel 3.
6. ↑ Doris Schattschneider: The Plane Symmetry Groups: Their Recognition and Notation. In: The American Mathematical Monthly. Band 85, Nr. 6, 1978, S. 439–450, doi:10.2307/2320063.

Weblinks

Commons: Symmetrie – Sammlung von Bildern, Videos und Audiodateien

• morenaments euc, Java Applet und Application. Behält gezeichnete Linienzüge beim Wechsel der Gruppe bei.
• Escher Web Sketch, Java Applet. Erlaubt neben dem Freihandzeichnen auch die Benutzung einzelner anderer Objekte.