Transitive Relation

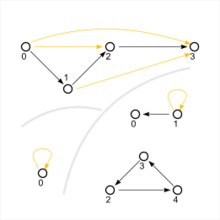Zwei transitive und eine nicht transitive Relation (rechts unten), als gerichtete Graphen dargestellt

Eine transitive Relation ist in der Mathematik eine zweistellige Relation R {\displaystyle R} $R$ auf einer Menge, die die Eigenschaft hat, dass für drei Elemente x {\displaystyle x} $x$ , y {\displaystyle y} $y$ , z {\displaystyle z} $z$ dieser Menge aus x R y {\displaystyle xRy} $xRy$ und y R z {\displaystyle yRz} $yRz$ stets x R z {\displaystyle xRz} $xRz$ folgt. Beispiele für transitive Relationen sind die Gleich- und die Kleiner-Relationen auf den reellen Zahlen, denn für drei reelle Zahlen x {\displaystyle x} $x$ , y {\displaystyle y} $y$ und z {\displaystyle z} $z$ mit x = y {\displaystyle x=y} $x=y$ und y = z {\displaystyle y=z} $y=z$ gilt immer auch x = z {\displaystyle x=z} $x=z$ , und aus x < y {\displaystyle x<y} $x<y$ und y < z {\displaystyle y<z} $y<z$ folgt x < z {\displaystyle x<z} $x<z$ .

Eine nicht transitive Relation heißt intransitiv (nicht zu verwechseln mit negativer Transitivität). Die Transitivität ist eine der Voraussetzungen für eine Äquivalenzrelation oder eine Ordnungsrelation.

Formale Definition

Ist M {\displaystyle M} $M$ eine Menge und R ⊆ M × M {\displaystyle R\subseteq M\times M} $R\subseteq M\times M$ eine zweistellige Relation auf M {\displaystyle M} $M$ , dann heißt R {\displaystyle R} $R$ transitiv, wenn (unter Verwendung der Infixnotation) gilt:

∀ x , y , z ∈ M : x R y ∧ y R z ⇒ x R z . {\displaystyle \forall x,y,z\in M:xRy\land yRz\Rightarrow xRz.}

\forall x,y,z\in M:xRy\land yRz\Rightarrow xRz.

Darstellung als gerichteter Graph

Jede beliebige Relation R {\displaystyle R} $R$ auf einer Menge M {\displaystyle M} $M$ kann als gerichteter Graph aufgefasst werden (Beispiel siehe oben). Die Knoten des Graphen sind dabei die Elemente von M {\displaystyle M} $M$ . Vom Knoten a {\displaystyle a} $a$ zum Knoten b {\displaystyle b} $b$ wird genau dann eine gerichtete Kante (ein Pfeil a ⟶ b {\displaystyle a\longrightarrow b} $a\longrightarrow b$ ) gezogen, wenn a R b {\displaystyle aRb} $aRb$ gilt.

Die Transitivität von R {\displaystyle R} $R$ lässt sich im Graphen nun so charakterisieren: Wann immer zwei Pfeile aufeinanderfolgen ( a ⟶ b ⟶ c {\displaystyle a\longrightarrow b\longrightarrow c} $a\longrightarrow b\longrightarrow c$ ), gibt es auch einen Pfeil, der Anfangs- und Endknoten direkt verbindet ( a ⟶ c {\displaystyle a\longrightarrow c} $a\longrightarrow c$ ) (so auch im Hasse-Diagramm).

Eigenschaften

Die Transitivität einer Relation R {\displaystyle R} $R$ erlaubt auch Schlüsse über mehrere Schritte hinweg (wie man leicht durch vollständige Induktion zeigt): a R b 1 R b 2 R … R b n R c ⟹ a R c {\displaystyle a\,R\,b_{1}\,R\,b_{2}\,R\,\dots \,R\,b_{n}\,R\,c\implies a\,R\,c} $a\,R\,b_{1}\,R\,b_{2}\,R\,\dots \,R\,b_{n}\,R\,c\implies a\,R\,c$
Mit Hilfe der Verkettung ∘ {\displaystyle \circ } $\circ$ von Relationen lässt sich die Transitivität auch durch die folgende Bedingung charakterisieren: R ∘ R ⊆ R {\displaystyle R\circ R\subseteq R} $R\circ R\subseteq R$
Ist die Relation R {\displaystyle R} $R$ transitiv, dann gilt dies auch für die konverse Relation R − 1 {\displaystyle R^{-1}} $R^{-1}$ . Beispiele: die zu ≤ {\displaystyle \leq } $\leq$ konverse Relation ist ≥ {\displaystyle \geq } $\geq$ , die zu < {\displaystyle <\ } $<\$ konverse ist > {\displaystyle >\ } $>\$ .
Sind die Relationen R {\displaystyle R} $R$ und S {\displaystyle S} $S$ transitiv, dann gilt dies auch für ihre Schnittmenge R ∩ S {\displaystyle R\cap S} $R\cap S$ . Diese Aussage lässt sich von zwei Relationen auf den Durchschnitt ∩ i ∈ I R i {\displaystyle \cap _{i\in I}R_{i}} $\cap _{i\in I}R_{i}$ einer beliebigen Familie von transitiven Relationen verallgemeinern.
Zu jeder beliebigen Relation R {\displaystyle R} $R$ gibt es eine kleinste transitive Relation S {\displaystyle S} $S$ , die R {\displaystyle R} $R$ enthält, die sogenannte transitive Hülle von R {\displaystyle R} $R$ .
Beispiel: R {\displaystyle R} $R$ sei die Vorgängerrelation auf der Menge der natürlichen Zahlen, es gelte also a R b :⟺ a = b − 1 {\displaystyle a\,R\,b:\Longleftrightarrow a=b-1} $a\,R\,b:\Longleftrightarrow a=b-1$ . Die Relation R {\displaystyle R} $R$ selbst ist nicht transitiv. Als transitive Hülle von R {\displaystyle R} $R$ ergibt sich die Kleiner-Relation < {\displaystyle <\ } $<\$ .

Beispiele

Wichtiges Beispiel aus der Volkswirtschaftslehre ist das Nichtsättigungsaxiom.

Ordnung der reellen Zahlen

Aus a > b und b > c folgt a > c

Die Kleiner-Relation < {\displaystyle <\ } $<\$ auf den reellen Zahlen ist transitiv, denn aus x < y {\displaystyle x<y} $x<y$ und y < z {\displaystyle y<z} $y<z$ folgt x < z {\displaystyle x<z} $x<z$ . Sie ist darüber hinaus eine strenge Totalordnung.

Ebenso sind die Relationen > {\displaystyle >\ } $>\$ , ≤ {\displaystyle \leq \ } $\leq \$ und ≥ {\displaystyle \geq \ } $\geq \$ transitiv.

Gleichheit der reellen Zahlen

Die gewöhnliche Gleichheit = {\displaystyle =\ } $=\$ auf den reellen Zahlen ist transitiv, denn aus x = y {\displaystyle x=y} $x=y$ und y = z {\displaystyle y=z} $y=z$ folgt x = z {\displaystyle x=z} $x=z$ . Sie ist darüber hinaus eine Äquivalenzrelation.

Die Ungleichheitsrelation ≠ {\displaystyle \neq } $\neq$ auf den reellen Zahlen ist hingegen nicht transitiv: 3 ≠ 5 {\displaystyle 3\neq 5} $3\neq 5$ und 5 ≠ 3 {\displaystyle 5\neq 3} $5\neq 3$ , aber 3 ≠ 3 {\displaystyle 3\neq 3} $3\neq 3$ gilt natürlich nicht.

Teilbarkeit der ganzen Zahlen

Die Teilbarkeitsrelation | {\displaystyle |} $|$ für ganze Zahlen ist transitiv, denn aus a | b {\displaystyle a|b} $a|b$ und b | c {\displaystyle b|c} $b|c$ folgt a | c {\displaystyle a|c} $a|c$ . Sie ist darüber hinaus eine Quasiordnung. Bei der Einschränkung auf die Menge der natürlichen Zahlen erhält man eine Halbordnung.

Nicht transitiv ist zum Beispiel die Teilerfremdheit. So sind 12 {\displaystyle 12} $12$ und 5 {\displaystyle 5} $5$ teilerfremd, ebenso 5 {\displaystyle 5} $5$ und 9 {\displaystyle 9} $9$ , jedoch haben 12 {\displaystyle 12} $12$ und 9 {\displaystyle 9} $9$ den gemeinsamen Teiler 3 {\displaystyle 3} $3$ .

Teilmenge

Die Teilmengenbeziehung ⊆ {\displaystyle \subseteq } $\subseteq$ zwischen Mengen ist transitiv, denn aus A ⊆ B {\displaystyle A\subseteq B} $A\subseteq B$ und B ⊆ C {\displaystyle B\subseteq C} $B\subseteq C$ folgt A ⊆ C {\displaystyle A\subseteq C} $A\subseteq C$ . Darüber hinaus ist ⊆ {\displaystyle \subseteq } $\subseteq$ eine Halbordnung.

Nicht transitiv ist zum Beispiel die Disjunktheit von Mengen. So sind die Mengen { 1 , 2 } {\displaystyle \lbrace 1,2\rbrace } $\lbrace 1,2\rbrace$ und { 3 } {\displaystyle \lbrace 3\rbrace } $\lbrace 3\rbrace$ disjunkt, ebenso { 3 } {\displaystyle \lbrace 3\rbrace } $\lbrace 3\rbrace$ und { 1 , 4 } {\displaystyle \lbrace 1,4\rbrace } $\lbrace 1,4\rbrace$ , nicht aber { 1 , 2 } {\displaystyle \lbrace 1,2\rbrace } $\lbrace 1,2\rbrace$ und { 1 , 4 } {\displaystyle \lbrace 1,4\rbrace } $\lbrace 1,4\rbrace$ (da sie das Element 1 gemeinsam haben).

Parallele Geraden

In der Geometrie ist die Parallelität von Geraden transitiv: Sind sowohl die Geraden g 1 {\displaystyle g_{1}} $g_{1}$ und g 2 {\displaystyle g_{2}} $g_{2}$ parallel als auch die Geraden g 2 {\displaystyle g_{2}} $g_{2}$ und g 3 {\displaystyle g_{3}} $g_{3}$ , dann sind auch g 1 {\displaystyle g_{1}} $g_{1}$ und g 3 {\displaystyle g_{3}} $g_{3}$ parallel. Darüber hinaus ist die Parallelität eine Äquivalenzrelation.

Implikation in der Logik

In der Logik gilt die Transitivität bezüglich der Implikation, wobei dies in der Prädikatenlogik auch als Modus barbara bekannt ist:

Aus A ⇒ B {\displaystyle A\Rightarrow B} $A\Rightarrow B$ und B ⇒ C {\displaystyle B\Rightarrow C} $B\Rightarrow C$ folgt A ⇒ C {\displaystyle A\Rightarrow C} $A\Rightarrow C$ (vergleiche auch: Schnittregel).

Die Implikation definiert eine Quasiordnung auf den Formeln der jeweils betrachteten Logik.

Weblinks

Transitivity. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 1-55608-010-7 (englisch, encyclopediaofmath.org).

Einzelnachweise

↑ Seymor Lipschutz, Marc Lipson: Schaum's Outline of Discrete Mathematics. McGraw Hill Professional, 1997, ISBN 978-0-07-136841-4, S. 33 (google.de ).
↑ a b Seymor Lipschutz, Marc Lipson: Schaum's Outline of Discrete Mathematics. McGraw Hill Professional, 1997, ISBN 978-0-07-136841-4, S. 34 (google.de ).
↑ Dov M. Gabbay, John Woods: The Rise of Modern Logic: from Leibniz to Frege. Elsevier, 2004, ISBN 978-0-08-053287-5, S. 509 (google.de ).
↑ Seymor Lipschutz, Marc Lipson: Schaum's Outline of Discrete Mathematics. McGraw Hill Professional, 1997, ISBN 978-0-07-136841-4, S. 35 (google.de ).